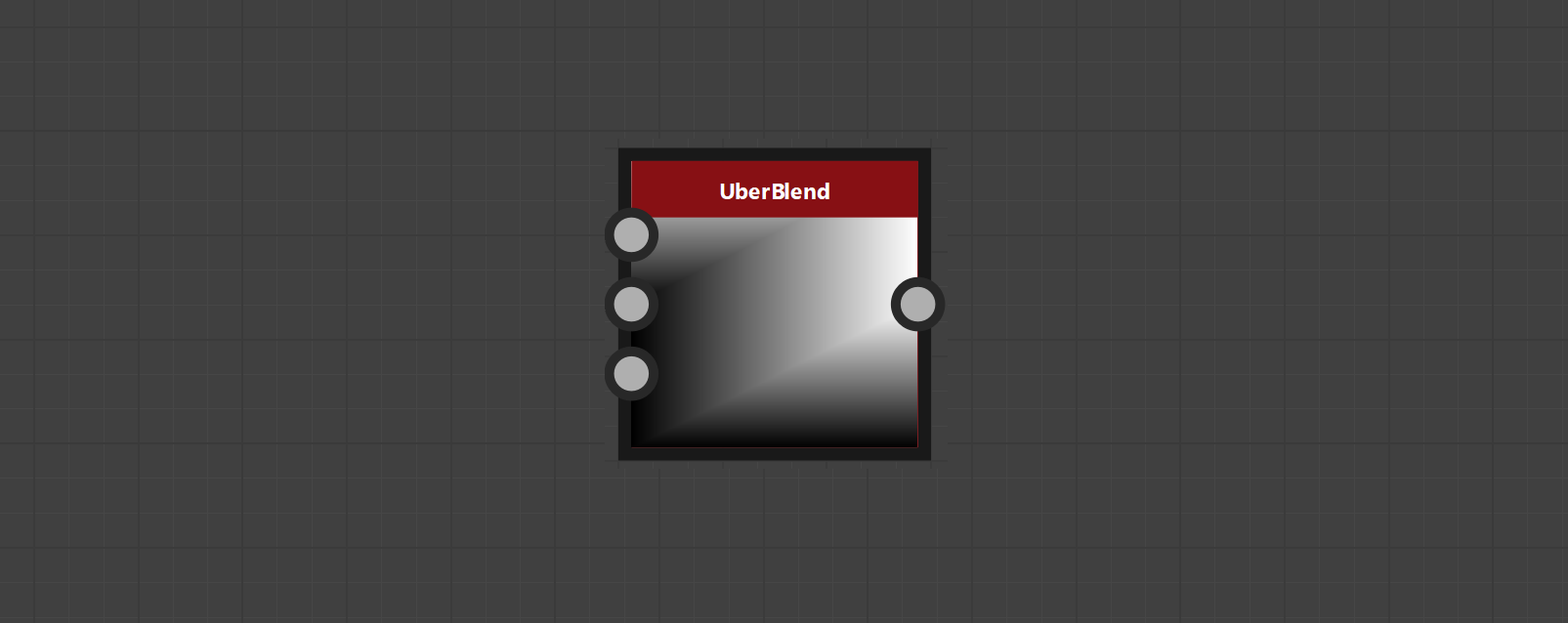
After my first article on blending-modes, the topic somehow stuck with me, so I got pulled down the associated rabbit hole. To process my experiences on the journey back to reality, I created an “almighty” 😉 node for blending layers. It contains 47 different blending modes for grayscale and RGB(A) and three additional blending modes specifically for NormalMaps. However, so that you don’t lose track of how the various blending modes work, the rest of the article is intended as a reference work.

About UberBlend

I named the node UberBlend because I have never come across such a complete collection of blending modes before. Are so many blending modes really necessary? Probably not, but why not try them out to achieve better results. My aim is to increase the probability of “happy accidents”.

UberBlend is available in different versions. Once as an all-in-one node “UberBlend” and once divided into “UberBlend Grayscale”, “UberBlend Color” and “UberBlend Normals”. The reason for this is that custom nodes in Adobe Substance 3D Designer are subject to certain limitations, so unfortunately I can’t offer the best user experience with the all-in-one solution. The limitation is that you have to manually choose between grayscale and color, because I unfortunately haven’t found a way to take over the convenience of the integrated blend node, where the color mode is based on the background input. As a result, you can get two additional inputs when switching between Grayscale and Color if you have already connected the inputs of the previously selected color mode.

What functionalities does UberBlend generally offer?

• 47 different general blending modes; more details can be found in the next section
• 3 special blending modes for NormalMaps
• “Advanced” mode for RGB(A) inputs, in which settings can be made per color channel
• Familiar functionalities of the integrated blend node, such as support for input masks, setting the opacity, …

I am currently planning to create versions of UberBlend that can be used with Substance 3D Painter and Photoshop. Since both have their own challenges, these versions will be released separately.

For the impatient: Click here to download

Blending-Modes

The following table provides a comparison of the different blending modes:

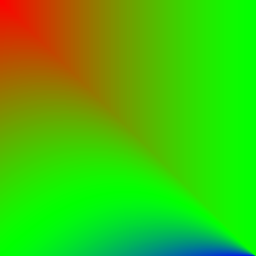
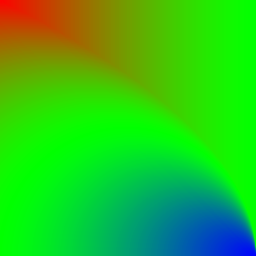
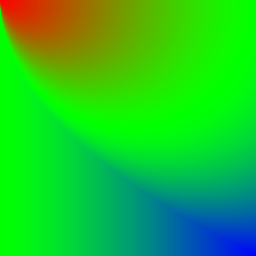
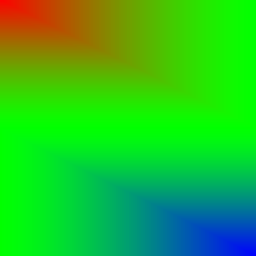
• In the Brightness column, you can see the blend result of the two known grayscale gradients, with the horizontal gradient acting as the background and the vertical gradient as the foreground.
• In the Brightness difference column, you can see the changes in brightness between the blend result and the original background. Lightenings are reddish and darkenings are colored bluish. Greenish areas have little or no change.
• The table is sorted alphabetically. If anyone has an idea for a better sorting, please let me know.

Blending Mode	Brightness	Brightness difference
Arctan	\(p_\text{new} = 2\pi * \text{arctan}(\frac{p_\text{bg}}{p_\text{fg}})\)
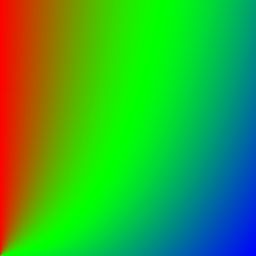Average	\(p_\text{new} = \frac{p_\text{fg} + p_\text{bg}}{2}\)
Bleach	\(p_\text{new} = (1 - p_\text{fg}) + (1 - p_\text{bg}) - 1\)
Bright	\(p_\text{new} = 1 - \text{Dark}(1 - p_\text{fg}, 1 - p_\text{bg})\)
Burn	\(p_\text{new} = 1 - \frac{1 - p_\text{fg}}{p_\text{bg}}\)
Burn (Reverse)	\(p_\text{new} = 1 - \frac{1 - p_\text{bg}}{p_\text{fg}}\)
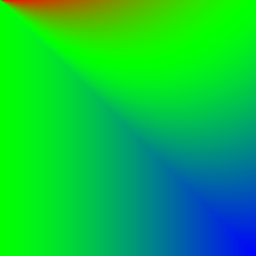Burn (Soft)	\(p_\text{new} = \begin{cases} \frac{1}{2} * \frac{p_\text{fg}}{1 - p_\text{bg}} & p_\text{bg} + p_\text{fg} \lt 1 \\\\1 - (\frac{1}{2} * \frac{1 - p_\text{bg}}{p_\text{fg}}) & \text{sonst}\end{cases} \)
Dark	\(p_\text{new} = p_\text{bg}p_\text{fg} + p_\text{fg} - p_\text{fg}^2 \)
Darken / Min	\(p_\text{new} = \text{Min}(p_\text{bg}, p_\text{fg})\)
Darken (Illusions.hu)	\(p_\text{new} = \log_2(1 + \frac{\frac{p_\text{bg}}{1- p_\text{fg}}}{8})\)
Difference	\(p_\text{new} = |p_\text{bg} - p_\text{fg}|\)
Divide	\(p_\text{new} = \frac{p_\text{bg}}{p_\text{fg}}\)
Dodge	\(p_\text{new} = \frac{p_\text{bg}}{1 - p_\text{fg}}\)
Dodge (Linear) / Add	\(p_\text{new} = p_\text{bg} + p_\text{fg}\)
Dodge (Reverse)	\(p_\text{new} = \frac{p_\text{fg}}{1 - p_\text{bg}}\)
Dodge (Soft)	\(p_\text{new} = \begin{cases} \frac{1}{2} * \frac{p_\text{bg}}{1 - p_\text{fg}} & p_\text{bg} + p_\text{fg} \lt 1 \\\\1 - (\frac{1}{2} * \frac{1 - p_\text{fg}}{p_\text{bg}}) & \text{sonst}\end{cases} \)
Exclusion	\(p_\text{new} = p_\text{bg} + p_\text{fg} - 2 p_\text{bg} p_\text{fg}\)
Freeze	\(p_\text{new} = 1 - (1 - p_\text{bg}) \frac{1 - p_\text{bg}}{p_\text{fg}}\)
Gamma (Bright)	\(p_\text{new} = 1 - (1 - p_\text{bg}) ^ \frac{1}{1 - p_\text{fg}}\)
Gamma (Dark)	\(p_\text{new} = p_\text{bg} ^ \frac{1}{p_\text{fg}}\)
Gamma (Light)	\(p_\text{new} = p_\text{bg} ^ {p_\text{fg}}\)
Geometric Mean	\(p_\text{new} = \sqrt{p_\text{bg} p_\text{bg}}\)
Glow	\(p_\text{new} = \frac{p_\text{fg} p_\text{fg}}{p_\text{bg}}\)
Grain (Extract)	\(p_\text{new} = p_\text{bg} + (1 - p_\text{fg}) - \frac{1}{2}\)
Grain (Merge)	\(p_\text{new} = p_\text{bg} + p_\text{fg} - \frac{1}{2}\)
Heat	\(p_\text{new} = 1 - (1 - p_\text{fg}) \frac{1 - p_\text{fg}}{p_\text{bg}}\)
Lighten / Max	\(p_\text{new} = \text{Max}(p_\text{bg}, p_\text{fg})\)
Light (Hard)	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} & p_\text{fg} \lt \frac{1}{2} \\\\1 - (2 * (1 - p_\text{fg})(1 - p_\text{bg})) & \text{sonst}\end{cases} \)
Lighten (Illusions.hu)	\(p_\text{new} = 1 - \text{Darken (Illusions.hu)}(1 - p_\text{fg}, 1 - p_\text{bg})\)
Light (Linear) / Add Sub	\(p_\text{new} = p_\text{bg} + ((p_\text{fg} - \frac{1}{2}) * 2)\)
Light (Pin)	\(p_\text{new} = \begin{cases} \text{Min}(p_\text{bg}, 2 p_\text{fg}) & p_\text{fg} \lt \frac{1}{2} \\\\\text{Max}(p_\text{bg}, 2 p_\text{fg} - 1) & \text{sonst}\end{cases}\)
Light (Vivid)	\(p_\text{new} = \begin{cases} \text{Burn}(p_\text{bg}, 2 p_\text{fg}) & p_\text{fg} \lt \frac{1}{2} \\\\\text{Dodge}(p_\text{bg}, 2 p_\text{fg} - 1) & \text{sonst}\end{cases}\)
Multiply	\(p_\text{new} = p_\text{bg} * p_\text{fg}\)
Negation	\(p_\text{new} = 1 - |(1 - p_\text{bg}) - p_\text{fg}|\)
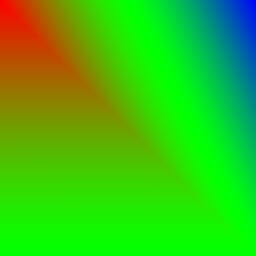Overlay	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} & p_\text{bg} \lt \frac{1}{2} \\\\1 - (2 (1 - p_\text{bg}) (1 - p_\text{fg})) & \text{sonst}\end{cases}\)
Parallel	\(p_\text{new} = \frac{2}{\frac{1}{p_\text{bg}}+\frac{1}{p_\text{fg}}}\)
Phoenix	\(p_\text{new} = \text{Min}( p_\text{bg}, p_\text{fg}) + (1 - \text{Max}(p_\text{bg}, p_\text{fg}))\)
Reflect	\(p_\text{new} = \frac{p_\text{bg} ^ 2}{1 - p_\text{fg}}\)
Screen	\(p_\text{new} = p_\text{bg} + p_\text{fg} - p_\text{bg} * p_\text{fg}\)
Shadow	\(p_\text{new} = 1 - ((1 - p_\text{bg}) p_\text{fg}) + \sqrt{1 - p_\text{fg}} \)
Softlight (PS, DS)	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} + p_\text{bg}^2 (1 - 2 p_\text{fg}) & p_\text{fg} \lt 0.5 \\\sqrt{p_\text{bg}} (2 p_\text{fg} - 1) + 2 p_\text{bg} (1 - p_\text{fg}) & \text{sonst}\end{cases}\)
Softlight (Illusions.hu)	\(p_\text{new} = p_\text{bg} ^ {(2 ^ {2 (0,5 - p_\text{fg} )})}\)
Softlight (PegTop)	\(p_\text{new} = (1 - 2 p_\text{fg}) * p_\text{bg} ^ 2 + 2 p_\text{bg} p_\text{fg} \)
Subtract	\(p_\text{new} = p_\text{bg} - p_\text{fg}\)

Even though blending of NormalMaps only rarely occurs within Substance 3D Designer, I thought that it might not hurt to integrate specialized blending modes. For this reason, I followed the really detailed and interesting article Blending in Detail and transferred the three “best” blending modes, i.e. whiteout blending, UDN blending and reoriented normal mapping.

The following two normal maps are used as test objects:

I have been thinking for a long time about how I can also write the respective NormalMap calculations as a formula. I hope I have found a comprehensible way. The shader-oriented variant can be found in the linked article Blending in Detail.

Blending Mode	Formula	Result
UDN	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * 2 - 1 \\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * 2 - 1 \\ \vec{r} &= \begin{pmatrix} \vec{p_\text{bg}}_x + \vec{p_\text{fg}}_x \\ \vec{p_\text{bg}}_y + \vec{p_\text{fg}}_y \\ \vec{p_\text{bg}}_z \end{pmatrix} \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)
Whiteout	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * 2 - 1 \\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * 2 - 1 \\ \vec{r} &= \begin{pmatrix} \vec{p_\text{bg}}_x + \vec{p_\text{fg}}_x \\ \vec{p_\text{bg}}_y + \vec{p_\text{fg}}_y \\ \vec{p_\text{bg}}_z * \vec{p_\text{fg}}_z \end{pmatrix} \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)
Reoriented Normal Mapping	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + \begin{pmatrix} -1 \\ -1 \\ 0 \end{pmatrix}\\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * \begin{pmatrix} -2 \\ -2 \\ 2 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}\\ \vec{r} &= \vec{p_\text{bg}} * (\vec{p_\text{bg}} \cdot \vec{p_\text{fg}}) - \vec{p_\text{fg}} * \vec{p_\text{bg}}_z \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)

So, before the download really comes, a direct comparison between the blending modes of the NormalMaps, as the results only show differences if you look directly.

UberBlend Download

I make the SBSAR from UberBlend available to all interested parties free of charge under CC0 1.0.

So you can actually do anything legal with it, as long as you don’t make me responsible for any mistakes. However, if you find any mistakes, I would be happy if you let me know so that I can correct them 😉

Further reading

Of course, I didn’t come up with all this information all by myself. Fortunately, there are people who have already prepared a lot of the information so that I could use them as sources. So if you want to find out more about the topic, you are welcome to visit the following pages:

• https://yahvuu.wordpress.com/2009/09/27/blendmodes1/
• https://blog.selfshadow.com/publications/blending-in-detail/