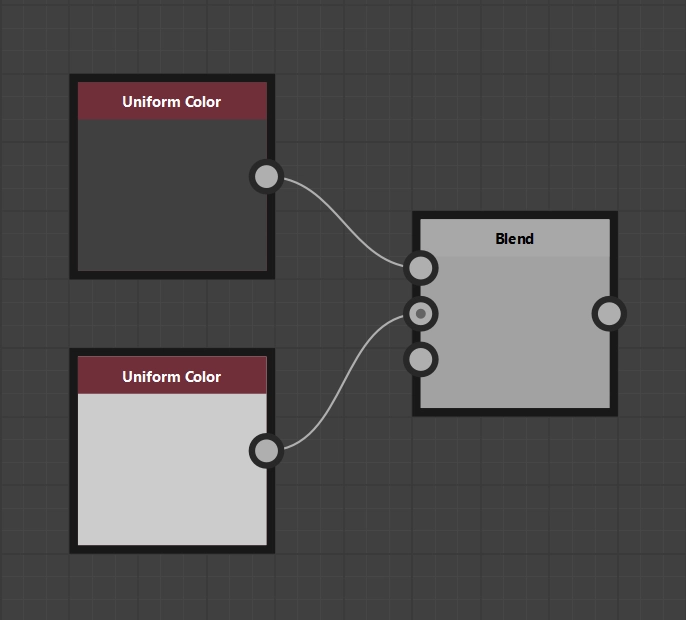
In the last article on blending modes, I had initially excluded the topic of opacity in order to look at it again separately, but unfortunately I forgot this separate consideration before publication. So this consideration is a bit more separate than I originally meant 😉
The opacity is generally independent of the selected blending mode. This value is used after executing the selected blending mode to set how the blending result is calculated with the background, i.e. how much the background is covered. 100% opacity means that the blending result has full opacity and represents the new overall result. 0% opacity, on the other hand, means that the background is applied unchanged. For all values in between, the ratio of both values is determined depending on the opacity setting, so that the following formula applies:
\(p_\text{opa} = O * p_\text{new} + (1 - O) * p_\text{bg}\)
- \(p_\text{opa}\)
- Pixel of the overall result
- \(O\)
- Opacity set between 0 and 1
- \(p_\text{new}\)
- Pixel of the blending result
- \(p_\text{bg}\)
- Background pixel
Examples
The following examples are always structured in the same way. First I define the values, then I insert them into the formula and finally the result is calculated.
Example 1
- Opacity \(O \mathrel{\unicode{x2254}} 1\)
- Pixel of the blending result \(p_\text{new} \mathrel{\unicode{x2254}} 0.25\)
- Background pixel \(p_\text{bg} \mathrel{\unicode{x2254}} 0.8\)
\(\begin{eqnarray} p_\text{opa} &=& O * p_\text{new} + (1 - O) * p_\text{bg} \\ &=& 1 * 0.25 + (1 - 1) * 0.8 \\ &=& 0.25 + 0 * 0.8 \\ &=& 0.25 + 0 \\ &=& 0.25 \\ \end{eqnarray}\)
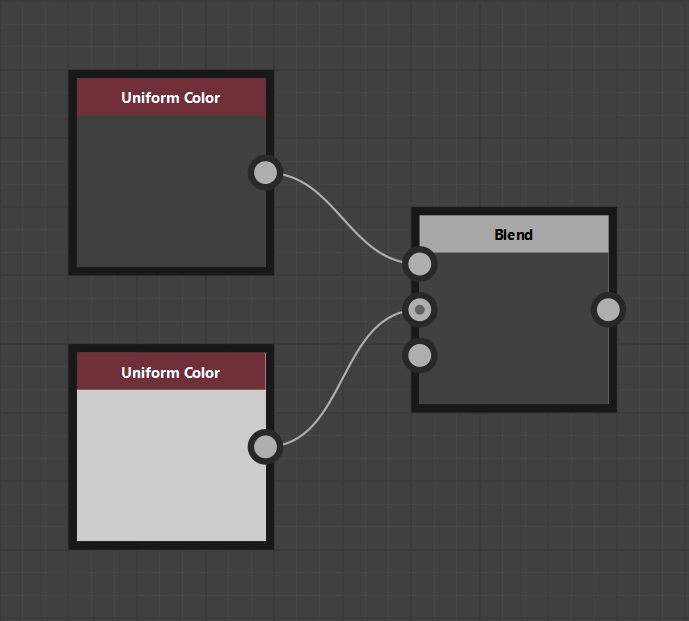
Example 1 (graphically)
Example 2
- Opacity \(O \mathrel{\unicode{x2254}} 0\)
- Pixel of the blending result \(p_\text{new} \mathrel{\unicode{x2254}} 0.25\)
- Background pixel \(p_\text{bg} \mathrel{\unicode{x2254}} 0.8\)
\(\begin{eqnarray} p_\text{opa} &=& O * p_\text{new} + (1 - O) * p_\text{bg} \\ &=& 0 * 0.25 + (1 - 0) * 0.8 \\ &=& 0 + 1 * 0.8 \\ &=& 0 + 0 \\ &=& 0.8 \\ \end{eqnarray}\)
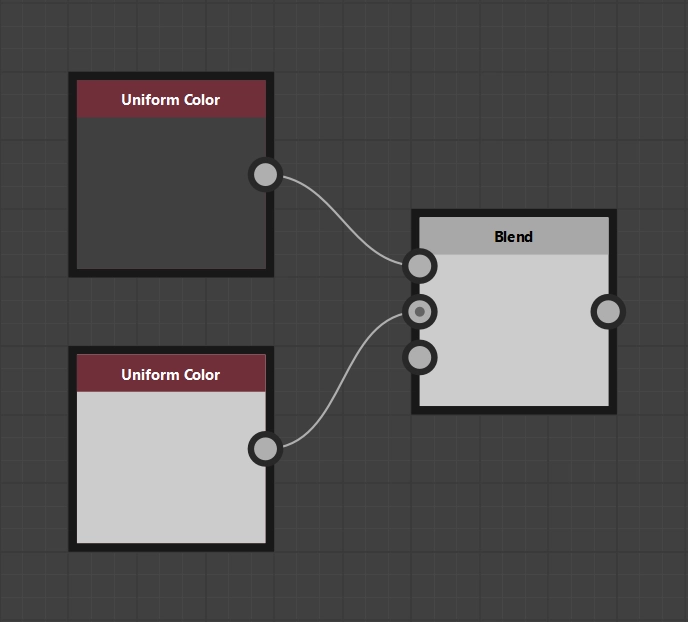
Example 2 (graphically)
Example 3
- Opacity \(O \mathrel{\unicode{x2254}} 0.3\)
- Pixel of the blending result \(p_\text{new} \mathrel{\unicode{x2254}} 0.25\)
- Background pixel \(p_\text{bg} \mathrel{\unicode{x2254}} 0.8\)
\(\begin{eqnarray} p_\text{opa} &=& O * p_\text{new} + (1 - O) * p_\text{bg} \\ &=& 0.3 * 0.25 + (1 - 0.3) * 0.8 \\ &=& 0.075 + 0.7 * 0.8 \\ &=& 0.075 + 0.56 \\ &=& 0.635 \\ \end{eqnarray}\)