Nach meinem ersten Artikel zum Thema Blending-Modes hat mich das Thema irgendwie nicht mehr losgelassen, sodass ich ins zugehörige Kaninchenbau gezogen wurde. Um meine Erlebnisse auf der Reise zurück in die Realität zu verarbeiten, habe ich einen “allmächtigen” 😉 Knoten für’s Blenden von Ebenen erstellt. Dieser enthält 47 verschiedene Blending-Modes für Graustufen und RGB(A) und drei zusätzliche Blending-Modes speziell für NormalMaps. Damit man aber nicht den Überblick über die Funktionsweise der verschiedenen Blending-Modes verliert, soll der restliche Artikel als Nachschlagewerk dienen.

Über UberBlend

Ich habe den Knoten UberBlend getauft, da mir bislang keine so vollständige Sammlung an Blending-Modes begegnet ist. Sind so viele Blending-Modes wirklich notwendig? Wahrscheinlich nicht, aber warum sollte man sie nicht ausprobieren, um so bessere Resultate erzielen zu können. Mein Ziel ist es, so die Wahrscheinlichkeit für “Happy Accidents” zu erhöhen.

Es gibt UberBlend in verschiedenen Versionen. Einmal als All-in-One-Knoten “UberBlend” und einmal aufgeteilt in “UberBlend Grayscale”, “UberBlend Color” und “UberBlend Normals”. Der Grund hierfür ist, dass eigene Knoten in Adobe Substance 3D Designer gewissen Beschränkungen unterliegen und ich daher mit der All-in-One-Lösung leider nicht die beste Benutzererfahrung bieten kann. Die Einschränkung ist dabei, dass man manuell zwischen Graustufen und Farbe wählen muss, da ich leider keine Möglichkeit gefunden habe, wie man bei eigenen Knoten den Komfort des integrierten Blend-Knotens übernimmt, bei dem sich der Farbmodus nach dem Hintergrundeingang richtet. Dies hat zur Folge, dass man beim Wechsel zwischen Grayscale und Color zwei zusätzliche Eingänge bekommen kann, wenn man die Eingänge des vorher ausgewählten Farbmodus bereits angebunden hatte.

Welche Funktionalitäten bietet UberBlend generell:

• 47 verschiedene allgemeine Blending-Modes; genauere Details findet ihr im nächsten Abschnitt
• 3 spezielle Blending-Modes für NormalMaps
• “Advanced” Modus für RGB(A)-Eingaben, in welchem pro Farbkanal Einstellungen vorgenommen werden können
• Gewohnte Funktionalitäten des integrierten Blend-Knotens, wie Unterstützung von Eingabemasken, Einstellen der Deckkraft, …

Aktuell plane ich, auch noch Versionen von UberBlend zu erstellen, die sich mit Substance 3D Painter und Photoshop nutzen lassen. Da beide ihre eigenen Hürden mit sich bringen, werden diese Versionen dann gesondert erscheinen.

Für alle Ungeduldigen: Hier geht es zum Download

Blending-Modes

Die folgende Tabelle soll einen Vergleich der verschiedenen Blending-Modes ermöglichen:

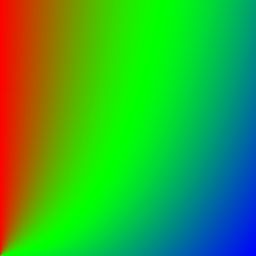
• In der Spalte Helligkeit sieht man das Blend-Resultat der beiden bekannten Graustufen-Gradienten, wobei der horizontale Gradient als Hintergrund und der vertikale Gradient als Vordergrund agiert.
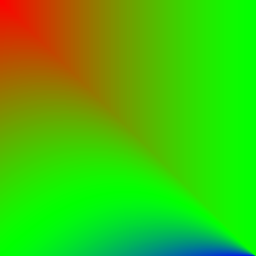
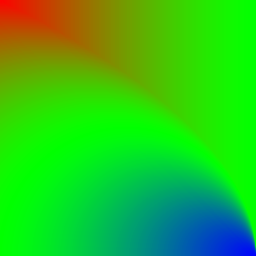
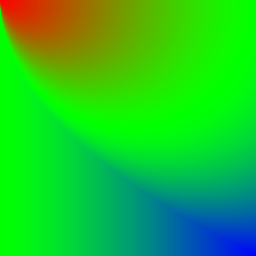
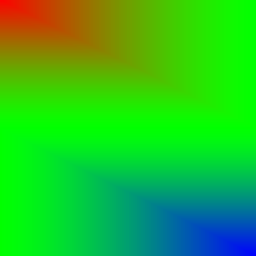
• In der Spalte Helligkeitsunterschied sieht man die Helligkeitsveränderungen zwischen dem Blendresultat und dem ursprünglichen Hintergrund. Aufhellungen sind rötlich und Abdunkelungen sind bläulich eingefärbt. Grünliche Bereiche haben entsprechend kaum bis keine Veränderungen.
• Die Tabelle ist alphabetisch sortiert. Sollte jemand eine Idee für eine bessere Sortierung haben, gerne bei mir melden.

Blending Mode	Helligkeit	Helligkeitsunterschied
Arctan	\(p_\text{new} = 2\pi * \text{arctan}(\frac{p_\text{bg}}{p_\text{fg}})\)
Average	\(p_\text{new} = \frac{p_\text{fg} + p_\text{bg}}{2}\)
Bleach	\(p_\text{new} = (1 - p_\text{fg}) + (1 - p_\text{bg}) - 1\)
Bright	\(p_\text{new} = 1 - \text{Dark}(1 - p_\text{fg}, 1 - p_\text{bg})\)
Burn	\(p_\text{new} = 1 - \frac{1 - p_\text{fg}}{p_\text{bg}}\)
Burn (Reverse)	\(p_\text{new} = 1 - \frac{1 - p_\text{bg}}{p_\text{fg}}\)
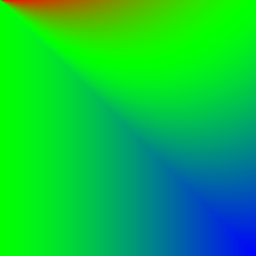Burn (Soft)	\(p_\text{new} = \begin{cases} \frac{1}{2} * \frac{p_\text{fg}}{1 - p_\text{bg}} & p_\text{bg} + p_\text{fg} \lt 1 \\\\1 - (\frac{1}{2} * \frac{1 - p_\text{bg}}{p_\text{fg}}) & \text{sonst}\end{cases} \)
Dark	\(p_\text{new} = p_\text{bg}p_\text{fg} + p_\text{fg} - p_\text{fg}^2 \)
Darken / Min	\(p_\text{new} = \text{Min}(p_\text{bg}, p_\text{fg})\)
Darken (Illusions.hu)	\(p_\text{new} = \log_2(1 + \frac{\frac{p_\text{bg}}{1- p_\text{fg}}}{8})\)
Difference	\(p_\text{new} = |p_\text{bg} - p_\text{fg}|\)
Divide	\(p_\text{new} = \frac{p_\text{bg}}{p_\text{fg}}\)
Dodge	\(p_\text{new} = \frac{p_\text{bg}}{1 - p_\text{fg}}\)
Dodge (Linear) / Add	\(p_\text{new} = p_\text{bg} + p_\text{fg}\)
Dodge (Reverse)	\(p_\text{new} = \frac{p_\text{fg}}{1 - p_\text{bg}}\)
Dodge (Soft)	\(p_\text{new} = \begin{cases} \frac{1}{2} * \frac{p_\text{bg}}{1 - p_\text{fg}} & p_\text{bg} + p_\text{fg} \lt 1 \\\\1 - (\frac{1}{2} * \frac{1 - p_\text{fg}}{p_\text{bg}}) & \text{sonst}\end{cases} \)
Exclusion	\(p_\text{new} = p_\text{bg} + p_\text{fg} - 2 p_\text{bg} p_\text{fg}\)
Freeze	\(p_\text{new} = 1 - (1 - p_\text{bg}) \frac{1 - p_\text{bg}}{p_\text{fg}}\)
Gamma (Bright)	\(p_\text{new} = 1 - (1 - p_\text{bg}) ^ \frac{1}{1 - p_\text{fg}}\)
Gamma (Dark)	\(p_\text{new} = p_\text{bg} ^ \frac{1}{p_\text{fg}}\)
Gamma (Light)	\(p_\text{new} = p_\text{bg} ^ {p_\text{fg}}\)
Geometric Mean	\(p_\text{new} = \sqrt{p_\text{bg} p_\text{bg}}\)
Glow	\(p_\text{new} = \frac{p_\text{fg} p_\text{fg}}{p_\text{bg}}\)
Grain (Extract)	\(p_\text{new} = p_\text{bg} + (1 - p_\text{fg}) - \frac{1}{2}\)
Grain (Merge)	\(p_\text{new} = p_\text{bg} + p_\text{fg} - \frac{1}{2}\)
Heat	\(p_\text{new} = 1 - (1 - p_\text{fg}) \frac{1 - p_\text{fg}}{p_\text{bg}}\)
Lighten / Max	\(p_\text{new} = \text{Max}(p_\text{bg}, p_\text{fg})\)
Light (Hard)	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} & p_\text{fg} \lt \frac{1}{2} \\\\1 - (2 * (1 - p_\text{fg})(1 - p_\text{bg})) & \text{sonst}\end{cases} \)
Lighten (Illusions.hu)	\(p_\text{new} = 1 - \text{Darken (Illusions.hu)}(1 - p_\text{fg}, 1 - p_\text{bg})\)
Light (Linear) / Add Sub	\(p_\text{new} = p_\text{bg} + ((p_\text{fg} - \frac{1}{2}) * 2)\)
Light (Pin)	\(p_\text{new} = \begin{cases} \text{Min}(p_\text{bg}, 2 p_\text{fg}) & p_\text{fg} \lt \frac{1}{2} \\\\\text{Max}(p_\text{bg}, 2 p_\text{fg} - 1) & \text{sonst}\end{cases}\)
Light (Vivid)	\(p_\text{new} = \begin{cases} \text{Burn}(p_\text{bg}, 2 p_\text{fg}) & p_\text{fg} \lt \frac{1}{2} \\\\\text{Dodge}(p_\text{bg}, 2 p_\text{fg} - 1) & \text{sonst}\end{cases}\)
Multiply	\(p_\text{new} = p_\text{bg} * p_\text{fg}\)
Negation	\(p_\text{new} = 1 - |(1 - p_\text{bg}) - p_\text{fg}|\)
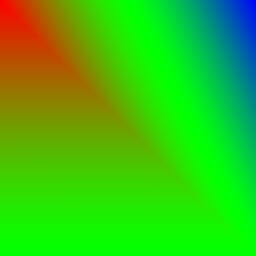Overlay	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} & p_\text{bg} \lt \frac{1}{2} \\\\1 - (2 (1 - p_\text{bg}) (1 - p_\text{fg})) & \text{sonst}\end{cases}\)
Parallel	\(p_\text{new} = \frac{2}{\frac{1}{p_\text{bg}}+\frac{1}{p_\text{fg}}}\)
Phoenix	\(p_\text{new} = \text{Min}( p_\text{bg}, p_\text{fg}) + (1 - \text{Max}(p_\text{bg}, p_\text{fg}))\)
Reflect	\(p_\text{new} = \frac{p_\text{bg} ^ 2}{1 - p_\text{fg}}\)
Screen	\(p_\text{new} = p_\text{bg} + p_\text{fg} - p_\text{bg} * p_\text{fg}\)
Shadow	\(p_\text{new} = 1 - ((1 - p_\text{bg}) p_\text{fg}) + \sqrt{1 - p_\text{fg}} \)
Softlight (PS, DS)	\(p_\text{new} = \begin{cases} 2 p_\text{bg} p_\text{fg} + p_\text{bg}^2 (1 - 2 p_\text{fg}) & p_\text{fg} \lt 0.5 \\\sqrt{p_\text{bg}} (2 p_\text{fg} - 1) + 2 p_\text{bg} (1 - p_\text{fg}) & \text{sonst}\end{cases}\)
Softlight (Illusions.hu)	\(p_\text{new} = p_\text{bg} ^ {(2 ^ {2 (0,5 - p_\text{fg} )})}\)
Softlight (PegTop)	\(p_\text{new} = (1 - 2 p_\text{fg}) * p_\text{bg} ^ 2 + 2 p_\text{bg} p_\text{fg} \)
Subtract	\(p_\text{new} = p_\text{bg} - p_\text{fg}\)

Auch wenn Blending von NormalMaps innerhalb von Substance 3D Designer nur selten vorkommt, dachte ich mir, dass es vielleicht trotzdem nicht schaden kann, darauf spezialisierte Blending Modes zu integrieren. Aus diesem Grund bin ich dem wirklich ausführlichen und interessanten Artikel Blending in Detail gefolgt und habe die drei “besten” Blending Modes transferiert, also Whiteout-Blending, UDN-Blending und Reoriented-Normal-Mapping.

Als Testobjekte müssen die folgenden zwei NormalMaps herhalten:

Ich habe lange Zeit darüber nachgedacht, wie ich die jeweiligen NormalMap-Berechnungen ebenfalls als Formel schreiben kann. Ich hoffe, ich habe eine verständliche Art und Weise gefunden. Die shaderorientierte Variante findet man im verlinkten Artikel Blending in Detail.

Blending Mode	Formel	Ergebnis
UDN	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * 2 - 1 \\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * 2 - 1 \\ \vec{r} &= \begin{pmatrix} \vec{p_\text{bg}}_x + \vec{p_\text{fg}}_x \\ \vec{p_\text{bg}}_y + \vec{p_\text{fg}}_y \\ \vec{p_\text{bg}}_z \end{pmatrix} \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)
Whiteout	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * 2 - 1 \\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * 2 - 1 \\ \vec{r} &= \begin{pmatrix} \vec{p_\text{bg}}_x + \vec{p_\text{fg}}_x \\ \vec{p_\text{bg}}_y + \vec{p_\text{fg}}_y \\ \vec{p_\text{bg}}_z * \vec{p_\text{fg}}_z \end{pmatrix} \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)
Reoriented Normal Mapping	\(\begin{align*} \vec{p_\text{bg}} &= \vec{p_\text{bg}} * \begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + \begin{pmatrix} -1 \\ -1 \\ 0 \end{pmatrix}\\ \vec{p_\text{fg}} &= \vec{p_\text{fg}} * \begin{pmatrix} -2 \\ -2 \\ 2 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}\\ \vec{r} &= \vec{p_\text{bg}} * (\vec{p_\text{bg}} \cdot \vec{p_\text{fg}}) - \vec{p_\text{fg}} * \vec{p_\text{bg}}_z \\ \vec{p_\text{new}} &= \frac{\vec{r}}{|\vec{r}|} * \frac{1}{2} + \frac{1}{2} \end{align*} \)

So, bevor nun wirklich der Download kommt, noch ein direkter Vergleich zwischen den Blending Modes der NormalMaps, da die Ergebnisse nur bei direktem Hinsehen Unterschiede aufzeigen.

UberBlend Download

Ich stelle das SBSAR von UberBlend allen Interessierten kostenlos unter der CC0 1.0 zur Verfügung.

Ihr dürft damit also eigentlich alles Legale tun, solange ihr mich nicht für etwaige Fehler verantwortlich macht. Solltet ihr Fehler finden, würde ich mich aber dennoch freuen, wenn ihr sie mir mitteilt, damit ich sie korrigieren kann 😉

Weitere Lektüre

Natürlich bin ich nicht von ganz allein auf all diese Erkenntnisse gekommen. Freundlicherweise gibt es Menschen, die viele der Informationen bereits gut aufbereitet haben, sodass ich sie als Quellen nutzen konnte. Falls ihr also mehr über das Thema erfahren wollt, könnt ihr gerne die folgenden Seiten besuchen:

• https://yahvuu.wordpress.com/2009/09/27/blendmodes1/
• https://blog.selfshadow.com/publications/blending-in-detail/